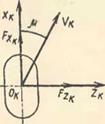
Особенности математической модели самолета как объекта управления

Задачи управления самолетом включают стабилизацию центра масс на заданной траектории и стабилизацию углового положения самолета относительно центра масс. Наиболее жесткие требования к точности управления предъявляются на этапах взлета и посадки. Ограничения на траектории движения при этом обусловлены нали­чием препятствий в секторах взлета и посадки. Препятствия нахо­дятся на земле, поэтому результатом исследования процессов взле­та и посадки должны быть траектории движения относительно земли. Иначе говоря, в число выходных переменных обязательно должны быть включены координаты центра масс самолета в земной системе координат.

В то же время выбор переменных состояния объекта в значи­тельной степени произволен, и выходные величины не обязательно должны совпадать с переменными состояния. Этим обусловлено большое число вариантов математических моделей, описывающих движение самолета в работах по аэродинамике и динамике полета [И. 24].

Далеко не все из них удобны для анализа процессов управ­ления, а некоторые просто некорректны при естественном предпо­ложении о разрывном характере возмущающих воздействий. В сзя — зи с этим необходимо остановиться подробнее на выборе математи­ческой модели управляемого объекта.

Будем исходить из следующих предположений. Самолет являет­ся жестким (изгибные колебания не учитываются). При этом его положение в пространстве однозначно задается шестью величина­ми— тремя координатами центра масс и тремя углами. При рас­смотрении процессов взлета и посадки анализируются сравнительно небольшие участки траекторий (до 20 …30 км), поэтому сферично­стью земли можно пренебрегать и пользоваться прямоугольной системой координат OgXgYgZg. Далее предполагается, что начало этой координатной системы находится на пересечении осевой линии с торцом ВПП, ось 0RXg представляет собой проекцию осевой ли­нии ВПП на плоскость горизонта, ось OgYg направлена вертикаль­но, а ось OgZg в плоскости горизонта вправо, если смотреть по на­правлению разбега (пробега). Влиянием вращения земли будем в дальнейшем пренебрегать и считать систему OgXgYgZg инерциаль­ной. При этом движение центра масс описывается простей —

ці нм векторным уравнением

і тс пі — масса самолета; r=(Xg, Yg, ZgY — радиус-век — iop центра масс в неполвижной системе координат (штрих обо — ніачаеттранспонирование);

F — суммарный вектор сил, чепствующнх на самолет.

Угловое положение самоле — I а задается тремя эйлеровыми s і іамн между осями неподвиж-

111,11 Ч связанной систем коорди — Рис. [ g Нормальная и связанная спе­ши [11]. Связанная система тема координат

OXYZ получается из неподвиж­ной O^XgYgZg путем параллельного переноса центра О в точку с і іхірдпнатами Xg, Yg, Zg и трех последовательных поворотов. Пер­мі поворот осуществляется на угол рысканья г|? вокруг оси, па­раллельной Ogyg, второй —на угол тангажа О вокруг оси Oz, тре­ти — на угол крена у вокруг оси Ох (рис. 1.6). Для перехода от неподвижной системы координат к связанной и обратно удобно пользоваться матрицей А направляющих косинусов (табл. 1.1).

Таблица 1.1 Связанная система Пііцмільная і нс ючга ох Л OY oz «(f-V, cos <Ь cos в sin 6 sin y — — cos ф sin 4 cos Y sin ф cos v 4- + cos ip sin ft sin у <><Г* sin ft cos ft cos y — cos ft sin у (>g/g — sin ф cos ft cos ф sin y 4- 4- sin & sin ft cos у cos ф cos Y — — sin ^ sin ft sin y Уравнение движения вокруг центра масс имеет вид [11] dK/dt=M, (1.5)

К вектор момента количества движения самолета, имеющий ‘ іуіощпс проекции на связанные оси:

K. V — IXWX I

К у=-ІхушхЛ-Іуи’у (І-6)

к

I моменты инерции самолета относительно связанных осей;

=y+Ф sin

шг=а cosy— Ф cos& sin y;

M — момент внешних сил, действующих на самолет.

Сила/7 и момент М, входящие в уравнения (1.4) и (1.5), обус­ловлены взаимодействием с воздушной средой (суммарная аэроди­намическая сила R и момент Мв), взаимодействием колес шасси с поверхностью ВПП на участках разбега и пробега (N и М^), весом G и тягой двигателей (Р и МР). Силы G и N удобно задавать про­екциями на неподвижные оси, а Р, R и моменты-—на связанные. В то же время моменты инерции, входящие в выражения (1.6), ока­зываются постоянными только относительно связанных осей. В свя­зи с этим уравнение сил (1.4) целесообразно записывать в проек­циях на неподвижные, а моментов (1.5) —на связанные оси, Отсю­да следует

F=G+N + MP+Ry, (18

М**М„+МР+МЯ.

Аэродинамические силы и моменты обычно представляются в форме [11]:

R=^qS (— Сг> С/. Сг) >

M — qS(ltnK, lmy, bAmz)’,

где q—pV2/2 — скоростной напор; р — плотность воздуха; S — пло­щадь крыла; Z — размах крыла; Ьл — средняя аэродинамическая хорда, d, ті — безразмерные аэродинамические коэффициенты сил и моментов.

Коэффициенты сил и моментов зависят от многих переменных: mt, Ci = f (а, % ю,., о,., М), (1.10)

где а — угол атаки (между проекцией воздушной скорости V на плоскость симметрии самолета XOY и осью ОХ) р— угол скольже­ния (между вектором V и плоскостью XOY) 6, — отклонения управляющих органов; М — число Маха.

Для интегрирования уравнений (1.4) и (1.5) величины V, а и р должны быть выражены через переменные состояния системы.

Очевидно:

V = ——W, (1.1)

dt

где XV = (Vxgi Wyg, Wzg) — вектор скорости — ветра, задаваемый как функция времени и координат W=W(t, г).

Уравнение плоскости симметрии самолета XOY в земной систе­ме координат имеет вид а3’г=0, где а3= (а13, а23, а33)’ — третий столбец матрицы А. В соответствии с этим угол скольжения можно определить из соотношения

sin3=(fl’V)/|V|. (1.11’)

Аналогично для угла атаки а получается соотношение

sin а = —(c2V)/|V| cos| (1.13)

іде о2= («12, «22, Й32)’ — второй столбец матрицы А.

Если аэродинамические коэффициенты в (1.9) заданы в полу — снязанной системе координат (11], они предварительно пересчиты­ваются в связанную преобразованием:

R = BRb M* = BM*lt (1.14)

1 те Ri, Mri — векторы суммарной аэродинамической силы и момен — іа в полусвязанной системе; R, Mr — соответствующие векторы в связанной системе; В —матрица перехода (табл. 1.2).

Таблица 1.2

(.вязанная система	Полусвязанная система
	ог„
ох	cos а	sin а	0
OY	— sin а	cos а	0
OZ	0	0	1

Рассмотрим теперь силы, обусловленные взаимодействием колес поверхностью ВПП. Для упрощения анализа будем пренебрегать инерционными нагрузками, обусловленными массой колес, и счи — м и,, что составляющая силы N, нормальная к поверхности ВПП, ІЛІІІІСПТ только от длины и скорости обжатия амортизаторов.

(ділу Ni, передаваемую на самолет через г-ю стойку шасси, iipi чпавим сначала проекциями на координатные оси Ок iXKiyK,2К Ось ОкіХкі представляет собой пересечение поверхности ВПП с "н костью, параллельной дискам колес. Ось ОкігК{ на поверхности НІНІ направлена перпендикулярно Ок {Хи і вправо, а ось Окіукі — шнірх. Если колеса г’-й стойки сохраняют контакт с поверхностью III III, сила

NiyK = Nі (lh /,), (1.15)

к 11 — длина і-й стойки шасси.

Іппііспмость Ni(U, І і) снимается экспериментально. При отрыве ‘ ч пт от поверхности ВПП Ni=0, и длина стойки /г меняется во арі меня в соответствии с решением уравнения

W,(/„/f) = 0. (1.16)

(діли N, rK характеризуют сопротивление качению колес

NiX к~ %i-Niyк, (1*17)

1 і" Ki*>Xi(VKi, |)Г і)—коэффициент сопротивления качению; VK~

І ірін и, івнжеиня колеса; рт — давление в тормозной системе.

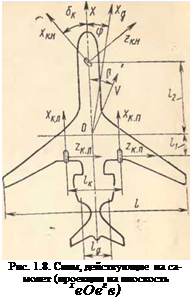
Сила Nizк появляется при движении колеса с углом увода цк (рис. 1.7):

N! zK~ (1.18)

где х = х(^к) —коэффициент боко­вой силы. Как показано в [2] для обычного трехстоечного шасси (рис. 1.8)

Рис. 1.7. Угол увода ко­леса

^к. п ~ Ф + (Zg + lk)tVк-п;

І’-к. л ~ Ф + teg + Лф)/ V’u. л;

Р’к. н ~ Ф “Ь^к. н’Ь (Zg — 1%ф)/Vк.„;

VK. n=V {xe+lKW+(ig+W‘i (U9)

Vm=sV’Ф/^)2+ (Zg-j — ЛІ*) ’

^K. H — xg~~{zg /2ф) .

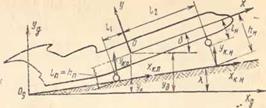
Индексы «п», «л» и «н» относятся соответственно к правой, ле­вой и носовой стойкам. Если поверхность ВПП имеет продольный уклон % и поперечный її (рис. 1.9 и 1.10), то пересчет сил NH в не­подвижную систему координат осуществляется с помощью матрицы J (табл. 1.3):

Ng=mK. (1.20)

Для вычисления моментов M. v необходимо сначала найти проек­ции сил Nn на связанные оси:

N=LNK. (1.21)

Коэффициенты матрицы L приведены в табл. 1.4. Из рис. 1.9 и 1.10

следует, что

?я *

Рис. 1.9. Силы, действую­щие на самолет (про­екции на плоскость хе^еУч)

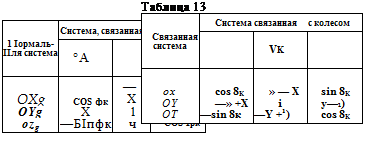^Nx—{Nяу №цу)Ік/*- №лгІІл Nnz/ln Nнг flH,

MNy=(N.IX — N„_t)lK/2—(JV]lz—Nnz)li~ IV Hzl2, (1.22)

Mnz=N N „хка — (N лу—№ ш/)^ +А^н;//2+ N ИГІія.

К этим соотношениям необходимо добавить еще геометрические, снизывающие расстояния Л,- от плоскости xOz до поверхности ВПП и юль г-й стойки шасси с переменными состояния (см. рис. 1.9 и 1.10):

hA=yg — ijgt —l (& — X) — f-1к (Y — 1l)/2; An=^-^0-/i(&-A)-ZK(Y-i1)/2; (1.23)

hH — Ug — ygi-r h® —

I і рн выводе соотношений (1.19) … (1.23) предполагалось, что углы X, 0, у, г) на разбеге и пробеге малы, так что косинусы их при­ми ил за единицу, а синусы считаются равными самим углам. Произ — |ц шипя этих углов за малостью не учитываются.

Когда колеса г-й стойки шасси катятся по поверхности ВПП, очевидно, что li = h;, и величина /,■ находится интегрированием си — I 1смы уравнений (1.4) … (1.5). Если

А/>ilm(hг), (1.24)

і 1C /,,„(//,) — решение уравнения (1.16), колеса отрываются от по­верхности ВПП. При этом дальнейшее изменение U определяется не решением уравнения (1.16), а в систему (1.4) … (1.5) подстав — лиоц я Ni = 0. Условие нового касания колес поверхности ВПП име — I вид /), </;. Начиная с этого момента снова полагается U=hi, и іммеїісчіие /,• находится интегрированием полной системы уравнений.

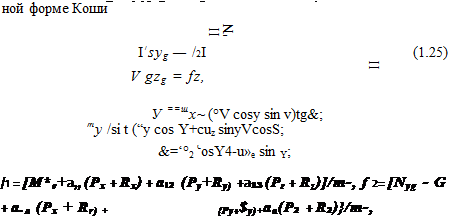
/з==[N*e + {Px + Rx) ~1~ “32 (Pe + Ry) + a33 (P2 + Rz))lrn-

/4= [Uy — /,) Iy*y + Uг — jx)Wj//2 + (IyMx + /XyMy)II2;

^Л + (Л-/Х) /^.J шг//2 — K/^-j-Z^Af,)//2; /б= [Л* К “ ш£) “ ~~ /л.) іі2 + MjIz;

I2 = IJy-Ixy М^Щ + Мр+М/,;

MRx—qSltnx (cti ^ %| 8h);

MRy—qSimy (a, Pi„xtV 8э( 8н);

с„г) 8в).

МРУ = (Р" ~ Рл) /,/2; Afpz = V PjhK)

Mnx== {N-"y ~ N"y) К12 — N,2lh-Nn2hn

MNy-*{Nnx — N„x) Ik/2+{Njiz + Nn г) ti _ дrKzl2,

= Naxka + Nuxliu — Шлу + Nn y)ix+Nuyi2 4_ NHXhH; Nix — Nt fv& — X) —Xi Cos 8kj _ t sin 8k.];

Nly = N і [2+X, Ф — X)+ХЛ/ (Ч — V)];

Ni2=Ni[(4 — sin 8K/ — ХіРкі cos8К/];

NXg= 2 (—*■ — *г cost—Хг^кі sin W^

N»g—2(1 ~l%i + N1’

Nze=2(T1+sin ~ cos w ^ *■*

Ni = Ni(l[, lt); хі=х,(Укі, Pn);

Zi=Z/(‘/K/); /=л, п, н; Фл=Ф„=<|»; 1івН*мі
PX = ^Pp Py = 2fjPp P, = 2VrJPJ>

Rx=—qScx, Ry=qScy; Rz=qScz; q=pV2/2; cx=cx(a); cy=cy(a, 6„); cz = cz(a, ?, 8H); VXg=VgXg-WXg-, VUg=Vgyg-Wyg

Vz= VgZg — VZg, V= (vlg + vlg+vlg)112;

sin ‘$=(0.^]/ Xg—a2ZV у g—a mV zg)tV’,
sin a=—(a12VXg+a2-yug+anVzgj/V cos?.

Здесь ф и фГ — углы установки двигателей в вертикальной и в горизонтальной плоскости. Выражения для коэффициентов ац даны и табл. 1.1.

Система (1.25), дополненная уравнениями (1.16) и геометри­ческими соотношениями (1.23), полностью описывает пространст­венное движение самолета как в воздухе, так и при разбеге или пробеге по ВПП.

І Ірактическое использование системы уравнений (1.25) при цифровом моделировании на ЦВМ, а также и при моделировании їм цифроаналоговых комплексах часто вызывает существенные нпруднения, связанные прежде всего с необходимостью вычисле­нии многочисленных тригонометрических функций. Эту систему не дастся интегрировать в реальном масштабе времени даже на са­мых быстродействующих ЦВМ, поэтому во многих случаях жела — 1<мц,1Н) пользоваться упрощенным описанием, позволяющим умень­шить временные затраты на интегрирование уравнений.

Пн этапах взлета и посадки существенное упрощение дает то иги ши гсльство, что каждый из углов ф, її и у может меняться лишь в небольших пределах, не более 15…20°. Угол отклонения передне — ю управляемого колеса ограничен еще более узкими предельными іііпчеііпямії. С учетом этого замена синусов самими углами дает ошибку, не превышающую 1 …2%, что вполне допустимо, так как і ой поп ь определения аэродинамических коэффициентов и характе-

ристик колес обычно еще меньше. В то же время замена косинуса единицей или пренебрежение произведением синусов может дать ошибку порядка 5… 10%, что не всегда допустимо, поэтому в разло­жениях нелинейных функций желательно сохранять члены второго порядка малости, пренебрегая членами более высокого порядка, т. е. полагать sin х&х; cos х«1 — х2/2. При этом матрица А (см. табл. 1.1) приобретает вид табл. 1.5. Соответственно, упрощаются остальные выражения в (1.25), и время интегрирования уравнений уменьшается более, чем на порядок.

Если углы меняются в более узких пределах (до 10°), целесооб­разно считать косинусы, равными единице и пренебрегать произве­дениями синусов. Кроме того, нужно учитывать, что всегда Ixu<g. Ix, Ixy^Iy. Наконец, практически всегда > V Ug, VXg^>VZg.

Таблица 1.5 Нормальная систем і Связанная система oz ox ОУ OgXg 0 gY g OgZg 1 _(4й+&2)/2 в -ф 1 — (»2 + Y2)/2 Y — h Ф» 1 -(ф2 + у2)/2

С учетом этого систему (1.25) можно заменить приближенной:

Vgxg — f\ ‘J, x = /4′ Xg— ^sxg" Y = y’.v>

^gug~ /а» wy ~f 5> Ug—Vgiig1 t=my > (1.26)

VgZg—/зі tuz— /бі Zg—Iу gUgi ®— "’г’

/i=12 (—^—Х/іакіФ/) N Ry^-{-Rz’>lm

/2=12 N і — 2 PjJr$RxJrPy~~VPz/,n’’

/3= (2 01 — Ni + 2 ?r jpi — Ф 2 P)- ФЯ*+y — Ry + RzMm

/4= m, — N„) lj2 — (Л — у — (Nahx-Nuhu) +

+(РЛ — Pn) i., <p/2+$£//«,]//,;

/5= [(» — X — ХГ) (IV„ — ЛГЛ) IJ2 + (Л — Y — Хг1^.г) (A^+Af,,) h ~

— I1! — Y — Zh^k. h Wj + (pi, — P,1) I,/2 + qSlrriy 111 tJ

/e= NJi — (Nz—N,) /г+<d — >0 2 AV/:—2 —

~’Lp)hAiJrQSbAmzIIz

q=?VV2; =

— [v — «4) ~

«=» — [Vgyg -+Y {Vgzg — W, g)]І

fti = !V= !V= І+ (Vgzg ~ 1Ы IVgxj

Ри=<Н“8к. н -~(Vgzg — t?’y)/Vgxg’ N і —Nidi, }[); j { 111 при (/,•); //,=/,;

1 hmVi) при ill > hm (!,)'<

k-V„t-XV„~l,{.,-V„t + I 2;

K — V„t-W„t-h(•,-V,:,,

*.= *„,I) •

Система (1.26) описывает пространственное движение самолета и не распадается на две независимые группы уравнений. Однако на этапе предварительного исследования обычно удобнее рассмат­ривать раздельно процессы продольного и бокового движения, что позволяет получить более «обозримые» результаты. При этом надо иметь в виду, что изменение параметров продольного движения зна­чительно сильнее влияет на боковое, чем параметры бокового дви­жения влияют на продольное. Поэтому начинать следует с анализа продольного движения. Если в уравнениях для VgXg, Vgyg, (oz, xg,

ij8 и О системы (1.26) положить у=))=р=|Лг = 0, Nn=N„=NT/2, они решаются независимо от остальных. В результате получаются функции VgXg{t), Vgyg(t),uz{t), xg(t), ijg(t), 0(0- Считая эти функ­ции известными, т. е. полагая, что параметры продольного движе­ния меняются по программе, можно решать теперь независимо ос­тавшуюся группу из шести уравнений, описывающих боковое дви­жение. Однако нельзя забывать, что полученные таким путем ре­зультаты носят предварительный характер. Связь между продоль­ным и боковым движениями осуществляется не только через дина­мику объекта, но и через систему управления. Особенно сильно она проявляется в режиме штурвального управления, так как свойства человека-оператора при управлении одноканальным или многока­нальным объектом существенно различны. Поэтому для окончатель­ных выводов необходима проверка полученных результатов модели­рованием полной системы уравнений пространственного движения.

Уравнения особенно упрощаются, если ограничиться исследова­нием движения самолета в воздухе. При этом исчезают в уравнени­ях (1.26) слагаемые, содержащие силы реакции колес. Для малых отклонений от установившегося режима движения вполне допусти­ма линеаризация уравнений. Разложив в ряды по степеням прира­щений bVgXg, ДVgygi ДWXg, b. Wyg, A(i)z, ДО, Да, Д6В, АР правые части уравнений (1.26), получим следующую линеаризованную
систему уравнений продольного движения (знаки приращений А для краткости опускаются):

VgXg=а„ (VgXg — WXg) + ап (I/gVg — Wyg)+avb+bnP;

Vgyg = «21 (VgXg — WXg) + «22 (VgBg — Vуg) + «27» + bnP vz = «61 (VgXg— W+P + «62 <VRUg— Wуg) + «66w2 +«67» + ^61^+^628,0

xg=VgXg (1.27)

yg=Vg4g’

^ = ,0Z,

flu = — QoS [2,(^0+»o+o) + (Сх-^ЪцСу)]!mVn
«12=<7о‘^ (с-г+»о«г/)/«г’1/,0′
a17= — q0S (cx+ &ocl + c^m; bn = 1 /да;
a21=q0s [2 (c^o -»Q^o)+ °o -*<fl)]lmV0;
fl22= —<7(+ (fiy »0«-r)/«^l+’
fl27 == <7o5 (+ — »(A’ — ^o)/OT + Pol>n;

(’2і = (сРд+»о)/^;

a61 =?0S6A (2отг0+%maz)/IzV0

«62 — — q^Sb^rrizI IZV 0;

«66= —^mpVo/tnl-, «67= — «62^ o! ^61 = —Лд/7г;

/b62= —a&V</nfclm’z

Vo—VgXgQ— U+^o! ®о=(1^гі/го — WygOi/Vfr Аналогично для бокового движения получим систему уравнений: VgZg=a, M (У gzg — У zg) + «звФ+«39 Y + (>зз+

Шх = fl43 (Vgzg — Wzg) + «44и3Д — + °45UV "Ь «48^ + «49Ї + ^н+^э!

йу = а5ъ {VgZg-WZg) +«84“х + «SSV+ «5(4 + «59Ї + +38н + Мэ’.

Zg = VgZg

^‘V

= шх>

aw=QoSclmVQ, аза — Язз^О’

аз9=4,йS (Суп — cVу/1/У0)/т;

^зз= ®зяCzH/Cz> Я4з=^д5/ш^//д. Ко; Я44=Я43Vоітіх^Іffix; Я45 = йцШх^ітхх; а48“а43^о! а49== —акУ У 643=(ЦціПхЧтІ; /;44=; a53=q0Slml/IyV0 a54=a53V0mwu*/ml

а55—а5*тУУІтУХі О5В = а53^0;

я5д=—Ядзі/у^о; Ь53=а^ту»/тІ

654 = «58 т-и’І ті

Полученные уравнения позволяют исследовать процессы управ­ления самолетом при малых отклонениях от установившегося ре­жима движения.

Глава 2